Climate Change and Tornadoes
Is there a link? New analysis shows no increase in tornado power.
With this past weekend’s devastating tornadoes killing over 88 in the Midwest United States, there is renewed debate over whether or not global warming and human caused climate change is causing an increase in the frequency and intensity of tornadoes in the US. “This is going to be our new normal, and the effects that we’re seeing from climate change are the crisis of our generation,” says FEMA administrator Deanne Criswell.
President Biden has tasked the EPA with investigating this issue. However, the US government National Center for Environmental Information (NCEI a division of NOAA), has already collected an extensive database of all tornadoes in the US since 1950; thus you might be tempted to conclude there already was an obvious answer to the question of whether or not tornadoes are increasing in frequency and intensity. But you would be wrong!
When you search the NOAA website for information on tornadoes you'll find Figure 1 below. This plot clearly shows that the number of recorded tornadoes in United States has significantly increased since 1950.
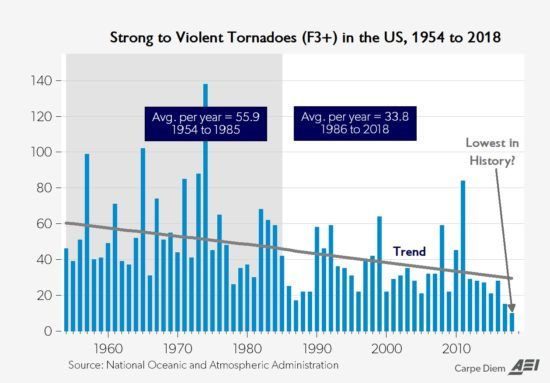
As others have reported for many years, this simple plot is misleading, as different tornado classification schemes have been implemented and new technologies like Doppler radar have made it possible for the United States Weather Service to identify more tornadoes per year. Many of the newly identified tornadoes are small. As prominent climate change alarmism skeptic, Dr. Roy Spencer, pointed out in a 2018 online post, the frequency of severe tornadoes (F3 and higher on the Fujita scale) actually shows a decreasing trend! See Figure 2.
So what's going on here? Is it possible that we're having more tornadoes but the frequency of large ones is decreasing? Doubtful. One hypothesis, which I think is much more likely, is that as time progressed throughout the record period, it became more likely that large tornadoes were segregated into constituent smaller tornadoes (F2 or lower) whenever the tornado damage was not continuous.
To circumvent this issue, along with avoiding the subjectiveness of the Fujita scale (especially for tornadoes early in the database which were given F or EF scores well afterwards), I have analyzed the raw tornado data in the NOAA database to calculate a new metric, Cumulative Tornado Length per year (see Figure 3), which is the sum of the length of travel for all recorded tornadoes in a year. The recorded tornado length is the one parameter in the database that is the least sensitive to measurement uncertainty and changes in measurement protocol (tornado width measurement protocols changed over time). This metric also has the advantage that it should be less sensitive compared to simple tornado count to the numerous small tornadoes that have been added to the record in more recent years.
Figure 3 shows there is a relatively small but positive trend in the Cumulative Tornado Length (CTL) per year. To check the sensitivity of this metric to the presence of numerous small, recent tornadoes in the database, I recalculated CTL filtering out tornadoes with lengths below 5, 10 and 50 miles, see Figures 4 , 5 and 6 respectively below.
Figures 4, 5 and 6 support Dr. Roy Spencer's observation of decreasing severe tornadoes over time but this appears due to the segregation of tornadoes into smaller constituent tornadoes. I will update this Substack post in future with specific examples, but for now it's worth noting that the years 2014, 2016, and 2018 had no tornadoes recorded in the database with path lengths over 50 miles, which seems incredible given that the tornado count and raw CTL those years exceed the corresponding values for the majority of the early record.
Conclusion: Figure 4 shows that the Cumulative Tornado Length per year, which is used here as a proxy for total tornado intensity over a year, is neither trending up nor down if we exclude tornadoes less than 5 miles in length. This provides strong evidence that claims of increasing tornado intensity are false so the premise that human caused warming is causing increased tornado intensity is also false.